講完機器學習的基礎，接下來是類神經網路訊號的傳遞函式。

• Activation Functions

Activation Functions(Transfer function)：Define the output of a node when given the inputs of the node.
依照輸入去給輸出的方程式都統一稱作Activation Functions。

類神經網路則是可以依照輸入值去判斷輸出的結果是inhibit(抑制)或excite(觸發)，可以是線性或非線性函數。

1. Sign function: f(n) = sign(n)
   之前寫python實作PLA有小小提到過，當n > 0的時候輸出1, n < 0的時候則是-1, n = 0則為的一個邏輯函數：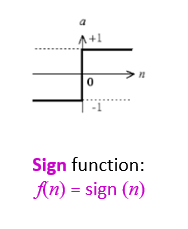
   

2. Linear function: f(n) = n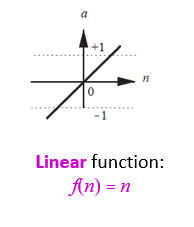
   

3. Logistic sigmoid function:f(n) = 1/(1+e^(−n) )
   將n帶入e，使f(n)的值趨近+1和0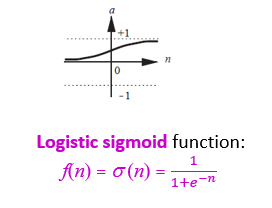
   

4. Hyperbolic Tangent Tanh function: f(n) = (e^n−e^(−n))/(e^n+e^(−n) )
   跟上面一樣用e去控制輸出的區間，但曲線漲幅較大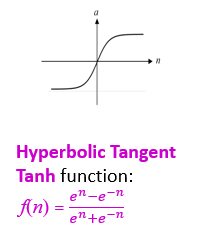
   

5. Rectified Linear Unit ReLU function: f(n) = max(0, n)
   簡單粗暴的判斷是否激發:是正數n就激發n，不是就輸出為0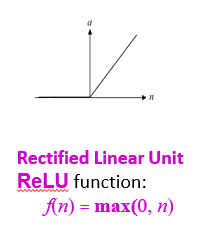
   

6. Leaky ReLU function: f(n) = max(0.01n, n)
   跟上面的激發狀態一樣，但抑制時會輸出0.01n的值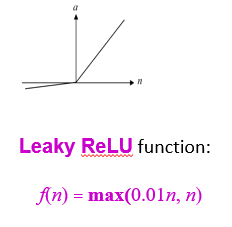
   

• Network Architectures

單層：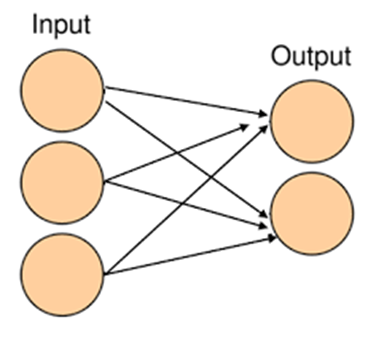

多層：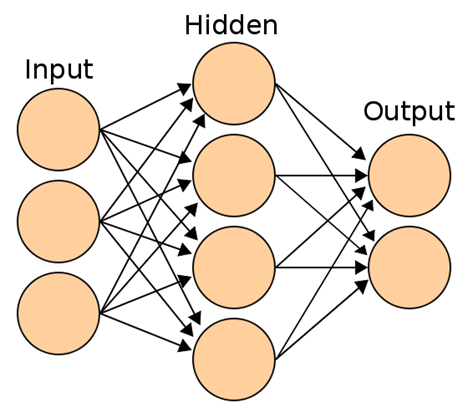

輸入後經過的層數在抵達輸出層前稱為隱藏層：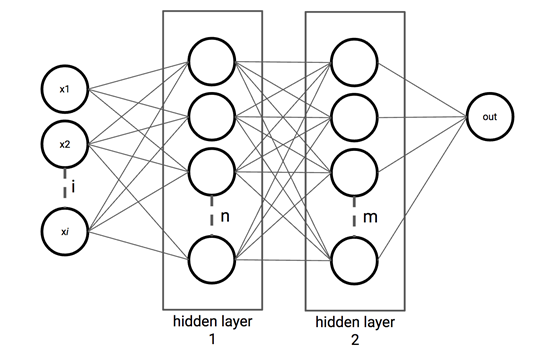

在數有幾層時輸入層不含在層數內，
因此上面的那個圖案隱藏層(2)+輸出(1)=三層